3. Задача семи мостов
Возможно ли найти такой маршрут, позволявший перейти все семь мостов, не ступив ни на один из них дважды
 |
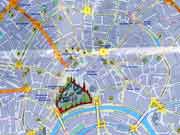
Задача семи мостов. Кенигсберг Как-то раз обещался рассказать про семь мостов Кёнигсберга – эта история должна быть хорошо известна среди математиков, а также быть на слуху для любознательных калининградцев. "Проблема семи мостов" легко нагугливается в сети, и единственным минусом множества посвящённых ей упоминаний мне представляется беллетризация текстов, отсутствие в них математического и логического анализа.
Что же это за задача, как она возникла и была разрешена.
Летопись Тевтонского ордена повествует нам, что в 1255 году великий магистр Поппо фон Остернa (Poppo von Osterna) вместе с чешским королём Оттокаром II Пржемыслом (Ottokar, Premysl Otakar), призванным на помощь в очередной крестовый поход против прусских язычников, заложили в нижнем течении реки Прегель замок, орденскую крепость, получившую название в честь Оттокара - Королевская гора – Кёнигсберг - Konigsberg. В 1257 году замок и будущий Альтштадт (Altstadt, Старый город) были обнесены рвом, в 1262 году после осады замка восставшими пруссами начинается кладка каменных стен. Почти сразу же по соседству появляются поселения - Альтштадт, Кнайпхоф (Kneiphof) и Лёбенихт (Lobenicht), каждое из которых получило права города в конце XIII – начале XIV века. Каждый из городов имел свой герб, у каждого были своё городское управление, свой суд и т.п., объединились они лишь в 1724 году, но обобщающее название Кёнигсберг закрепилось за ними со времени основания.
>>>
|
|
|
Задача семи мостов
Итак, мостов стало семь, а возможных маршрутов - тысячи, и некоторые горожане стали задаваться вопросом, возможно ли найти такой маршрут, позволявший перейти все семь мостов, не ступив ни на один из них дважды. Существовало даже поверье, согласно которому у проложившего такой маршрут должно исполниться загаданное желание.
Еще >>>
|
|
Леонард Эйлер
Портрет 1753 года работы Эмануэля Хандманна
Леонард Эйлер. Портрет 1753 года работы Эмануэля Хандманна
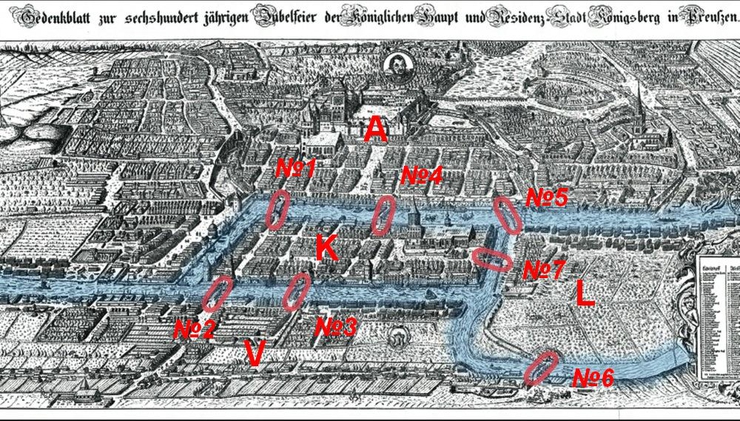
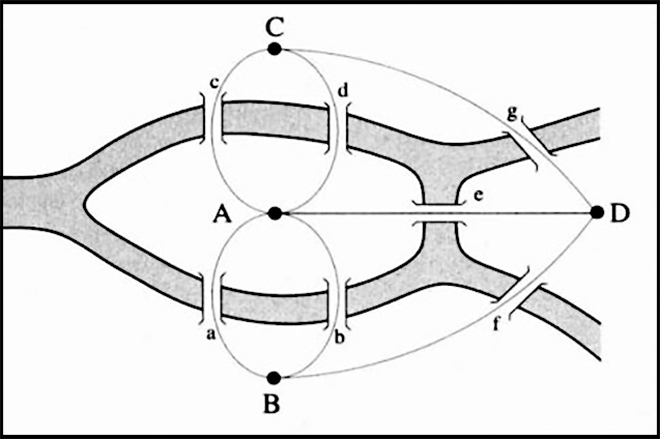
Решить задачу о Кёнигсбергских мостах удалось лишь в 1736 году, когда проблемой заинтересовался академик Санкт-Петербургской Академии, профессор высшей математики Леонард Эйлер (Leonhard Euler), фактически положивший начало новому разделу математики – теории графов. Интерес Эйлера к задаче был, вероятно, инициирован его перепиской с математиком и астрономом, будущим бургомистром Данцига (и почти однофамильцем) Карлом Элером (Carl Leonhard Gottlieb Ehler). На рисунке ниже – схема задачи из письма Элера – Эйлеру от 9 марта 1736 года.
отсюда >>>
|
|
 |
Уже 13 марта 1736 года Эйлер в письме к придворному астроному австрийских Габсбургов Джованни Маринони (Giovanni Jacobo Marinoni) сообщил, что "…нашел лёгкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершён такой обход через какое угодно число и как угодно расположенных мостов или не может", и изложил итальянцу это правило.
Авторы многих популярных статей, посвящённых семи мостам, не удосужившись заглянуть в оригинальную работу Эйлера "Solutio problematis ad geometriam situs pertinentis" ("Решение вопроса, связанного с геометрией положения"), датированную 1736 годом, и опубликованную в 1741 году в (первом русском) научном журнале-сборнике "Комментарии Петербургской Академии наук", сообщают, что тот абстрагировался от формы всех составляющих схемы и заменил их тем, что сегодня принято называть графом (рисунком в виде сети, что-то вроде того, что размещён чуть ниже) так, чтобы точки на суше стали вершинами, а мосты - дугами.
>>>
|
|
Схема задачи из статьи Эйлера
Мосты Кенигсберга
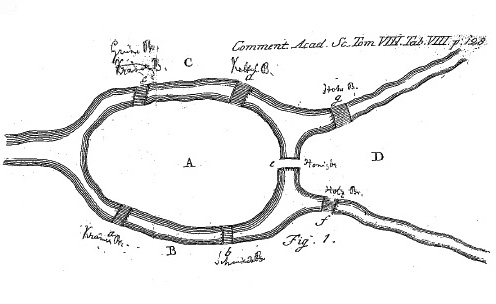 |
Схема задачи из статьи Эйлера
Эйлер предложил строгое аналитическое решение на основе следующих соображений.
Маршрут прохода по мостам можно представить последовательностью A-B-D-C… Число символов (вершин) в маршруте, который проходит по каждому мосту один раз, на 1 больше числа мостов в маршруте, поскольку каждая пара соседних вершин-символов соответствует переходу по одному мосту.
Основное соображение Эйлера заключалось в том, что если вершина (к примеру, А) не является концевой точкой маршрута, то она соответствует проходу по двум мостам, соединяющим вершину А с другими вершинами. А если вершина является концевой точкой – то проходу по одному мосту.
Отсюда следует, что если маршрут проходит по N мостам, соединяющим вершину А с другими вершинами, то символ А появляется в записи маршрута (N+1)/2 раз, если N нечётное (и при этом один раз А является концевой точкой маршрута), а если Nчётное – то либо N/2, либо N/2+1 раз (в последнем случае маршрут начинается и заканчивается символом А). Эйлер отмечает, что у каждого моста-дуги – два конца и что поэтому сумма чисел мостов, соединяющих каждую из вершин с остальными, вдвое превосходит общее число мостов и поэтому должна быть чётной; но тогда число вершин, в которых заканчивается нечётное число мостов, тоже должно быть чётным. Из этих соображений Эйлер выводит, что если общее число дуг-мостов в задаче равно M, а число вершин с нечётным числом мостов равно 2m, то запись маршрута, проходящего по всем мостам, должна содержать M+m символов, что больше M+1, если m>1.
В современной теории графов путь, проходящий по одному разу по всем дугам графа, называют эйлеровым путём, а замкнутый эйлеров путь – эйлеровым циклом. Условия существования таких путей очень просты:
1. Сеть, не имеющая нечётных вершин, допускает эйлеров цикл с началом в любой точке сети.
2. Сеть, имеющая две и только две нечётных вершины, обходится по эйлеровому пути, если начать движение с одной нечётной вершины и закончить его в другой.
3. Сеть, имеющую больше двух нечётных вершин, нельзя полностью обойти одним маршрутом.
Кёнигсбергская сеть имеет 4 вершины, в каждой из которых сходится нечётное число дуг-мостов: все вершины – нечётные (N для них равны 3,3,3 и 5), следовательно, требуемого маршрута – не существует.
Долгое время – свыше ста лет - статья Эйлера была единственной в своей области, и лишь во второй половине XIX века интерес к подобным задачам возродился в связи со знаменитой "проблемой четырёх красок", поставленной в 1852 году перед математиками Огастесом Де Морганом (Augustus de Morgan), а позже - с исследованиями электрических и логистических сетей, моделей кристаллов и молекулярных структур.
Эйлер в письме к Маринони указал, что достаточно построить ещё один мост через Прегель, и задача обхода одним маршрутом восьми мостов, каждого по одному разу, становится разрешимой. (В современных терминах это не будет эйлеров цикл, а будет эйлеров путь - по причине того, что две вершины останутся нечётными, и стартовать придётся в одной из них, а заканчивать обход всех восьми мостов – в другой.) В этой связи весьма популярной является легенда о появлении на карте Кёнигсберга восьмого моста, связывающего остров Ломзе с Форштадтом. Якобы на одном из приёмов приглашённые гости вздумали подшутить над кайзером Вильгельмом II, предложив тому решить задачу о мостах. Вильгельм, к всеобщему удивлению, заявил, что он решит задачу в считанные минуты, а на поданном листе бумаги написал: "Приказываю построить восьмой мост на остров Ломзе". Этот возведённый в 1905 году мост назвали "Императорским" (Kaiserbrucke).
|
|
Мосты Кенигсберга
Императорский мост, 1905 год
Императорский мост, 1905 год
Эйлер в письме к Маринони указал, что достаточно построить ещё один мост через Прегель, и задача обхода одним маршрутом восьми мостов, каждого по одному разу, становится разрешимой. (В современных терминах это не будет эйлеров цикл, а будет эйлеров путь - по причине того, что две вершины останутся нечётными, и стартовать придётся в одной из них, а заканчивать обход всех восьми мостов – в другой.)
В этой связи весьма популярной является легенда о появлении на карте Кёнигсберга восьмого моста, связывающего остров Ломзе с Форштадтом. Якобы на одном из приёмов приглашённые гости вздумали подшутить над кайзером Вильгельмом II, предложив тому решить задачу о мостах. Вильгельм, к всеобщему удивлению, заявил, что он решит задачу в считанные минуты, а на поданном листе бумаги написал: "Приказываю построить восьмой мост на остров Ломзе". Этот возведённый в 1905 году мост назвали "Императорским" (Kaiserbrucke).
|
|
Мосты Калининграда сегодня
Юбилейный мост
Мосты Калининграда сегодня. Юбилейный мост
Императорский мост был частично разрушен во время войны, но две опоры и центральный разводной пролёт простояли на реке до 80-х годов. 1 июля 2005 года, к 750-летию города на быках-опорах был выстроен новый мост, Юбилейный, внешне напоминающий Императорский. Также, как и у Медового, ограды моста скрыты под панцирем из замк?в.
|
|
No Comment? No! Comment! Более подробную информацию об этом можно узнать, кликнув по картинке...
|
|
|
Депутаты Госдумы нового созыва. Кенигсберг.. Россия. Задача семи мостов. Таежный пейзаж. Пьяный лес. Чудеса природы в России. Горы в тайге. Таежная речка. Сюда не ступала нога человека наверное лет сто.... Где находятся. Сайт. Фото. Картинка. Реферат. Реферат. Панорама кремля. Вид на кремль. Сайт. Фото.
|
|
|